Straight to the point

Periodically during the Covid-19 pandemic, CDC scientific staff have employed their available studies’ data to estimate the efficacy of current or recent versions of Covid-19 vaccines to reduce risk of testing positive for Covid-19. While the fact of “testing positive” has been somewhat controversial because of the secret PCR Ct threshold numbers involved that have allowed for uninfectious people with unrecognized Covid-19 from some weeks in the past to remain test-positive, my goal here is to illustrate CDC’s problematic epidemiologic methods that have substantially inflated the vaccine efficacy percents that they have reported.

Controlled epidemiologic studies fall into three and only three basic study designs. Either a total sample of subjects is sampled, and each subject is evaluated both for case status and previous exposure status—this is a cross-sectional study—or a sample of exposed people and a sample of unexposed people are followed to see who becomes a case and who a control—a cohort study—or a sample of cases and a sample of controls is obtained, and each subject evaluated for past exposure status—this is a case-control study. If a cohort study involves randomizing the subjects into those exposed and unexposed, this is a randomized controlled trial (RCT), but the study design is still cohort.

In a cross-sectional study and a cohort study, the risk of getting the outcome of interest (i.e., of being a case subject, here, testing positive) can be estimated for the exposed people by the number of cases among the exposed divided by the total number exposed. Similarly for the unexposed. What is of interest, the comparison of these two risks, the relative risk (RR), is the risk in the exposed divided by the risk in the unexposed. The RR estimates how much worse the risk is among the exposed compared to the unexposed. For a vaccine or other exposure that lowers risk, the RR will be less than 1.0.

Cross-sectional and cohort studies, by their sampling designs, allow the RR to be estimated from their data. However, case-control studies do not allow the outcome risks to be estimated, because changing the relative numbers of sampled cases vs controls affects what would be the risk estimates. Instead, case-control studies allow for the estimation of the odds of the outcome, not the risk. For example, 2:1 odds of an event happening. This value is unaffected by the sampling design. In case-control studies, the relative odds (or odds ratio, OR) of the outcome is estimated by the odds of the outcome among the exposed, divided by the odds among the unexposed.

For a vaccine, its efficacy is estimated as 1.0 – RR. For case-control study data which only estimate OR not RR, when does the OR approximate the RR accurately enough to be substituted in this formula? This question has a detailed epidemiologic history beyond the current scope, but in the simplest sense, the OR approximates the RR when in the population, cases are infrequent compared to controls.

Now to the CDC and its systematic epidemiologic errors. In a recent analysis, Link-Gelles and colleagues sampled a total of 9,222 eligible Covid-19-like symptomatic individuals seeking Covid-19 testing at CVS and Walgreen Co. pharmacies during September 21, 2023 through January 14, 2024. They assessed the previous vaccination status of each individual, as well as positivity of test result. By definition, this is a cross-sectional study, because individual numbers of cases and controls, or individual numbers of exposed (vaccinated) and unexposed (unvaccinated) were not sampled. Only the total number of subjects was sampled.

However, the investigators estimated the OR not the RR from these data, by using a statistical analysis method called logistic regression that allows the OR to be adjusted for various possible confounding factors. There is nothing wrong with using logistic regression and obtaining estimated ORs in any study design; the problem is using the OR value instead of the RR in the vaccine efficacy formula 1.0 – RR. Because the study design was cross-sectional, the investigators could have examined relative case occurrence in the population from their sampled numbers, but they did not appear to do this. In fact, cases comprised 3,295 of the total 9,222 sampled, 36%, which is not nearly small enough to use the OR as a substitute for the RR. This is true both among the exposed subjects (25%) and the unexposed (37%).

Nevertheless, it is possible to get a rough idea of how much this bad assumption affected the authors’ claimed overall 54% vaccine efficacy. The relevant numbers of subjects, shown in the table below, are stated in Tables 1 and 3 of the Link-Gelles paper. The RR calculation from these raw data is simple. The risk in the vaccinated is 281/1,125 = 25%; in the unvaccinated, it is 3,014/8,097 = 37%. The RR is the ratio of these two, 25%/37% = 0.67, thus the vaccine efficacy based on these raw data would be 1.0 – 0.67 = 0.33 or 33%.

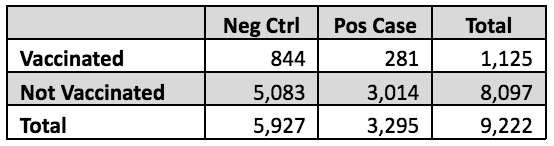
Similarly the OR can be estimated from these raw data as 0.56, which if used in the vaccine efficacy formula would give efficacy of 44%, appreciably different than the 33% efficacy as properly estimated by using the RR.

However, Link-Gelles et al. used the adjusted OR = 0.46 as obtained from their logistic regression analysis. This differs from the unadjusted OR = 0.56 by a factor of 0.46/0.56 = 0.82. We can use this adjustment factor, 0.82, to approximate what the raw RR would have been had it been adjusted by the same factors: 0.67*0.82 = 0.55. These numbers are shown in the table below, and demonstrate that the correct vaccine efficacy is approximately 45%, not the claimed 54%, and less than the nominal 50% desired level.

As an epidemiologist, I am unclear why my colleagues at the CDC would have mistakenly used the OR as a substitute for the RR when the required assumption for this substitution was not met and was easily checkable in their own data. They have made this error elsewhere (Tenforde et al.) where it also made a sizable difference in vaccine efficacy, approximately 57% as opposed to the claimed 82%. Perhaps the authors thought that the only method available to adjust for multiple confounding variables was logistic regression which uses the OR, but relative-risk regression for adjusting the RR has long been available in various commercial statistical analysis packages and is easily implemented (Wacholder).

It seems surprising to me that apparently none of the more than 60 authors between the Link-Gelles and Tenforde papers recognized that the sampling design of their studies was cross-sectional, not case-control, and thus that the proper parameter to use for estimating vaccine efficacy was the RR not the OR, and that the rare-disease assumption for substituting the OR for the RR was not met in their data. These studies therefore substantially overestimated the true vaccine efficacies in their results. This is not a purely academic issue, because CDC public health policy decisions can be derived from incorrect results such as these.

Source: Brownstone Institute Read the original article here: https://brownstone.org/